Такая вот мне задачка на ум пришла. Решения я не знаю, потому что с расчетами у меня всегда туго было, но, думаю, наши математики быстро найдут решение и ответ.
Суть задачи - у коллекционера моделей автомобилей в масштабе 1:18 появилась идея - засунуть в такую модель маленькую модельку (как, знаете, в реальных машинах иногда водители запихивают в свой Жигуль модель Феррари просто для понта), с тем, чтобы эта модель была в масштабе 1:18 к уже имеющейся "большой" модели. Вопрос - каким должен быть реальный масштаб "маленькой" модели, при условии, что обе модели изображают один и тот же автомобиль?
Меня интересует не только ответ, но и решение, потому что, имхо, просто умножить 18 на 18 это как-то слишком очевидно и просто.
Полная версия этой страницы: Логические задачи
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63
Дак, как бы, 1 : 324 и будет, неча сложности выдумывать.
Цитата(Darkmoon @ 30 Nov 2012, 09:43) 
потому что, имхо, просто умножить 18 на 18 это как-то слишком очевидно и просто.
если бы все решения были неочевидные и запутанные, то люди сидели бы сейчас в пещерах. в лучшем случае - с каменными инструментами и огнем.
Пара задачек:
1. Стрелок стреляет по мишени. Вероятность попадания в цель для каждого выстрела - 75%. Какова вероятность того, что стрелок попадет в цель ровно 1 раз, если он выполнил 3 выстрела (то есть попадет ровно 1 раз в серии из трех выстрелов).
2. В игре можно купить сундук с ценностями за 100 монет. Если открыть его при помощи ключа стоимостью 10 монет, он превратится во второй сундук с шансом 80% (ключ тратится, в случае неудачи сундук не изменяется). Если открыть второй сундук вторым ключом стоимостью 25 монет, то он превратится в третий сундук с шансом 60% (ключ тратится, в случае неудачи сундук превращается в первый). Аналогично третий сундук можно улучшить до четвертого ключом стоимостью 50 монет с шансом 40% (в случае неудачи - откат до второго). Какова стоимость четвертого сундука?
1. Стрелок стреляет по мишени. Вероятность попадания в цель для каждого выстрела - 75%. Какова вероятность того, что стрелок попадет в цель ровно 1 раз, если он выполнил 3 выстрела (то есть попадет ровно 1 раз в серии из трех выстрелов).
2. В игре можно купить сундук с ценностями за 100 монет. Если открыть его при помощи ключа стоимостью 10 монет, он превратится во второй сундук с шансом 80% (ключ тратится, в случае неудачи сундук не изменяется). Если открыть второй сундук вторым ключом стоимостью 25 монет, то он превратится в третий сундук с шансом 60% (ключ тратится, в случае неудачи сундук превращается в первый). Аналогично третий сундук можно улучшить до четвертого ключом стоимостью 50 монет с шансом 40% (в случае неудачи - откат до второго). Какова стоимость четвертого сундука?
Цитата
1. Стрелок стреляет по мишени. Вероятность попадания в цель для каждого выстрела - 75%. Какова вероятность того, что стрелок попадет в цель ровно 1 раз, если он выполнил 3 выстрела (то есть попадет ровно 1 раз в серии из трех выстрелов).
3*0,75*0,25*0,25 = 0,140625.
И это не логическая задачка, а банальный типовой пример из курса теорвера
2. Ради (максимум) 15 монет пусть кто-нибудь другой чешет затылок.
Я решил за час.
В ЛС могу ответ дать, если интересно будет
Вот 2 задачи!
1) Можно ли клетки бесконечного плоского листа клетчатой бумаги раскрасить в черный и белый цвет так, чтобы каждая прямая, параллельная линиям сетки, пересекала конечное число белых клеток, а каждая непараллельная - конечное число черных?
2) Можно ли разбить трехмерное пространство на синие и зеленые кубики (все одинакового размера) так, чтобы каждая горизонтальная и вертикальная плоскость пересекала конечное число синих кубиков, а каждая наклонная - конечное число зеленых кубиков?
1) Можно ли клетки бесконечного плоского листа клетчатой бумаги раскрасить в черный и белый цвет так, чтобы каждая прямая, параллельная линиям сетки, пересекала конечное число белых клеток, а каждая непараллельная - конечное число черных?
2) Можно ли разбить трехмерное пространство на синие и зеленые кубики (все одинакового размера) так, чтобы каждая горизонтальная и вертикальная плоскость пересекала конечное число синих кубиков, а каждая наклонная - конечное число зеленых кубиков?
1) Ох. Лень математически доказывать, поэтому объясню на пальцах:
Выбрать систему координат, начертить четыре квадартичные параболы с вершинами в начале координат, две с осями симметрии Ox и две с Oy, соответственно и закрасить черным клетки "внутри" них. Тогда каждая линия, не параллельная одной из осей координат, будет пересекать конечное число черных клеток, ограниченное параболами, а каждая линия, параллельная одной из осей координат, будет пересекать конечное число белых клеток, ограниченных черными клетками.
В принципе, можно взять не параболы, а четыре линии, проходящие через начало координат с шагом в 45 градусов и тоже закрасить "крестом". Но с параболами как-то попроще получается, потому что условий дополнительных к закрашиванию меньше.
Выбрать систему координат, начертить четыре квадартичные параболы с вершинами в начале координат, две с осями симметрии Ox и две с Oy, соответственно и закрасить черным клетки "внутри" них. Тогда каждая линия, не параллельная одной из осей координат, будет пересекать конечное число черных клеток, ограниченное параболами, а каждая линия, параллельная одной из осей координат, будет пересекать конечное число белых клеток, ограниченных черными клетками.
В принципе, можно взять не параболы, а четыре линии, проходящие через начало координат с шагом в 45 градусов и тоже закрасить "крестом". Но с параболами как-то попроще получается, потому что условий дополнительных к закрашиванию меньше.
Цитата(nosferatu @ 03 Apr 2013, 02:20)
1) Ох. Лень математически доказывать, поэтому объясню на пальцах:
Выбрать систему координат, начертить четыре квадартичные параболы с вершинами в начале координат, две с осями симметрии Ox и две с Oy, соответственно и закрасить черным клетки "внутри" них. Тогда каждая линия, не параллельная одной из осей координат, будет пересекать конечное число черных клеток, ограниченное параболами, а каждая линия, параллельная одной из осей координат, будет пересекать конечное число белых клеток, ограниченных черными клетками.
В принципе, можно взять не параболы, а четыре линии, проходящие через начало координат с шагом в 45 градусов и тоже закрасить "крестом". Но с параболами как-то попроще получается, потому что условий дополнительных к закрашиванию меньше.
Выбрать систему координат, начертить четыре квадартичные параболы с вершинами в начале координат, две с осями симметрии Ox и две с Oy, соответственно и закрасить черным клетки "внутри" них. Тогда каждая линия, не параллельная одной из осей координат, будет пересекать конечное число черных клеток, ограниченное параболами, а каждая линия, параллельная одной из осей координат, будет пересекать конечное число белых клеток, ограниченных черными клетками.
В принципе, можно взять не параболы, а четыре линии, проходящие через начало координат с шагом в 45 градусов и тоже закрасить "крестом". Но с параболами как-то попроще получается, потому что условий дополнительных к закрашиванию меньше.
Правильно, параболы подходят (сам так же решал).
Теперь осталось с пространством разобраться.
сделайте плиз рисунок... хочется лицезреть сие, хоть одним глазком...
конечность белых мне очевидна, а вот конечность черных нет
конечность белых мне очевидна, а вот конечность черных нет
Цитата(izrukvruki @ 03 Apr 2013, 09:30)
сделайте плиз рисунок... хочется лицезреть сие, хоть одним глазком...
конечность белых мне очевидна, а вот конечность черных нет
конечность белых мне очевидна, а вот конечность черных нет
Парабола рано или поздно обгоняет любую наклонную прямую, и будет выше нее, поэтому прямая будет пересекать только то, что внутри этих симметричных кривых (для конкретики, y = x^2 и y=-x^2. Тогда, пересечение наклонной с внутренностями графиков будет либо отрезком, либо пустым множеством, или точкой - lостаточно рассмотреть прямые y = kx. При этом, наклонная будет проходит через бесконечное число белых квадратов. А гориз. и верт. - наоборот, через бесконечное число черных)
Цитата(nosferatu @ 03 Apr 2013, 01:20)
Тогда каждая линия, не параллельная одной из осей координат, будет пересекать конечное число черных клеток, ограниченное параболами.
Цитата(izrukvruki @ 03 Apr 2013, 08:30)
сделайте плиз рисунок... хочется лицезреть сие, хоть одним глазком...
Цитата(tolich @ 03 Apr 2013, 12:33)
Цитата(nosferatu @ 03 Apr 2013, 01:20)
Тогда каждая линия, не параллельная одной из осей координат, будет пересекать конечное число черных клеток, ограниченное параболами.
Ну да, на этом все и строится - "бесконечность" клеток складывается из суммы "бесконечного" количества одних клеток и "конечности" других. При этом, каждая прямая будет пересекать "много" нужных клеток, но всегда конечное число.
Неужто никто ответов не знает?
Я только на 10ый вопрос, про мост, ответить не смог
Я только на 10ый вопрос, про мост, ответить не смог
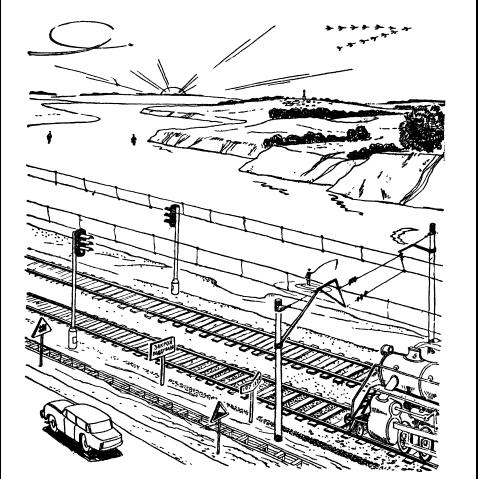
Я не могу понять что за таблички стоят на картинки...
1. месяц в реке отражается
2. солнце восходит ибо птици летят на юг ибо река замершая
3. птицы улетают ибо река во льду ибо по ней люди ходят - поздняя осень
4. уклон с верха картинки вправо, значит
5. зима же
6.
7.
8.9 - скоро будет пересечение с жел. дорогой и потом дорога пойдет вверх... значит дорога разойдется с ж/дорогой
10.
11. есть, ибо самолет видим в мертвой петле
12.
13. дует, видно по пару у паровоза
1. месяц в реке отражается
2. солнце восходит ибо птици летят на юг ибо река замершая
3. птицы улетают ибо река во льду ибо по ней люди ходят - поздняя осень
4. уклон с верха картинки вправо, значит
5. зима же
6.
7.
8.9 - скоро будет пересечение с жел. дорогой и потом дорога пойдет вверх... значит дорога разойдется с ж/дорогой
10.
11. есть, ибо самолет видим в мертвой петле
12.
13. дует, видно по пару у паровоза
Цитата(Iv @ 04 Apr 2013, 09:41)
Неужто никто ответов не знает?
Я только на 10ый вопрос, про мост, ответить не смог
Я только на 10ый вопрос, про мост, ответить не смог
Встречным поездам нужно тормозить состав, значит железную дорогу что-то пересекает (обычная дорога, например). Поскольку рядом с железной дорогой есть река, хоть и мелководная, то через неё должен быть проложен мост, следовательно мост тут есть.
Цитата(izrukvruki @ 04 Apr 2013, 10:14)
3. птицы улетают ибо река во льду ибо по ней люди ходят - поздняя осень
Река не замерзла, потому что у неё есть течение и там стоит рыбак, следовательно, раз по реке идут люди, то она мелководна и поэтому не судоходна.
Цитата(izrukvruki @ 04 Apr 2013, 10:14)
Я не могу понять что за таблички стоят на картинки...
Плохочитаемый ж/д знак - "закрой поддувало" :-)
Цитата(izrukvruki @ 04 Apr 2013, 10:14)
3. птицы улетают ибо река во льду ибо по ней люди ходят - поздняя осень
Это не люди, а бакены
Цитата(izrukvruki @ 04 Apr 2013, 10:14)
13. дует, видно по пару у паровоза
Вообще-то, паровоз едет, это видно по его колёсам. Так что не аргумент
Ещё одна такая же задачка.
Цитата(izrukvruki @ 04 Apr 2013, 10:14)
13. дует, видно по пару у паровоза
Паровоз движется, на светофоре зелёный.
Цитата(Iv @ 04 Apr 2013, 10:19)
Цитата(izrukvruki @ 04 Apr 2013, 10:14)
3. птицы улетают ибо река во льду ибо по ней люди ходят - поздняя осень
Это не люди, а бакены
Оу, тогда река судоходна.
П.С. Раз закрой поддувало, значит сейчас точно будет мост.
1. Если изврук прав и в реке отразился месяц, то меньше недели до новолуния.
2. Солнце либо на закате, либо на восходе, то есть на западе или на востоке. Журавлиный клин летит вправо, значит там юг, а прямо - восток. То есть у нас восход и ночь наступит не скоро.
3. Журавлиный клин. Осень.
4. Правый берег реки крутой - скорее всего река течёт от нас, на восток. Но, с другой стороны, рябь от рыбака идёт к нам, то есть река течёт к нам. Так что хз. Видимо, второй вариант правилен, так как крутой берег не стопроцентный признак направления течения реки.
5. Если это бакены, то река судоходна.
6. ???
7. ??? Светофор горит зелёным. Возможно, предыдущий поезд прошёл давно.
8. Знак крутого спуска на автодороге. Ж.д.-поезда не ходят по крутым спускам, значит пути авто и поезда разойдутся довольно скоро.
9. Шофёр готовится к спуску.
10. ???
11. Есть аэродром, откуда стартанул самолётик с лихим пилотом, выдающим петлю.
12. ???
13. ??? Бакены покачиваются, может ветер и есть.
2. Солнце либо на закате, либо на восходе, то есть на западе или на востоке. Журавлиный клин летит вправо, значит там юг, а прямо - восток. То есть у нас восход и ночь наступит не скоро.
3. Журавлиный клин. Осень.
4. Правый берег реки крутой - скорее всего река течёт от нас, на восток. Но, с другой стороны, рябь от рыбака идёт к нам, то есть река течёт к нам. Так что хз. Видимо, второй вариант правилен, так как крутой берег не стопроцентный признак направления течения реки.
5. Если это бакены, то река судоходна.
6. ???
7. ??? Светофор горит зелёным. Возможно, предыдущий поезд прошёл давно.
8. Знак крутого спуска на автодороге. Ж.д.-поезда не ходят по крутым спускам, значит пути авто и поезда разойдутся довольно скоро.
9. Шофёр готовится к спуску.
10. ???
11. Есть аэродром, откуда стартанул самолётик с лихим пилотом, выдающим петлю.
12. ???
13. ??? Бакены покачиваются, может ветер и есть.
Цитата(Etoprostoya @ 04 Apr 2013, 10:54)
2. Солнце либо на закате, либо на восходе, то есть на западе или на востоке. Журавлиный клин летит вправо, значит там юг, а прямо - восток. То есть у нас восход и ночь наступит не скоро.
3. Журавлиный клин. Осень.
Не обязательно именно журавлиный. И на север они тоже могут лететь, весной
4. крутой берег не стопроцентный признак направления течения реки.
Рыбак и ходить может, а вот крутой правый берег - более надёжный вариант
10. ???
Знак "Закрой поддувало" ставится перед деревянными мостами
12. ???
Да, т.к. для них здесь - подъем
3. Журавлиный клин. Осень.
Не обязательно именно журавлиный. И на север они тоже могут лететь, весной
4. крутой берег не стопроцентный признак направления течения реки.
Рыбак и ходить может, а вот крутой правый берег - более надёжный вариант
10. ???
Знак "Закрой поддувало" ставится перед деревянными мостами
12. ???
Да, т.к. для них здесь - подъем
Цитата(Terraniux @ 04 Apr 2013, 11:31)
Пока все думают, вот еще.
Сравните числа.
и 
Вечером выложу решение, если ранее не решите.
Сравните числа.
и Вечером выложу решение, если ранее не решите.
Пусть 
, 
. Тогда 
. Преобразуем последнее выражение: 
, пользуясь тем, что 
. В итоге много чего сокращается, кроме первой и последней дроби, для которой нету n+1. В итоге имеем, 
, . Тогда . Преобразуем последнее выражение: , пользуясь тем, что . В итоге много чего сокращается, кроме первой и последней дроби, для которой нету n+1. В итоге имеем, Цитата(Terraniux @ 04 Apr 2013, 14:34)
Пока все думают, вот еще.
Сравните числа.
и 
Вечером выложу решение, если ранее не решите.
Сравните числа.
и Вечером выложу решение, если ранее не решите.
Очевидно, что второе больше.
Корень из 1.5 примерно равен 1.225
Второе число будет стремиться к 1.17, можно примерно посчитать как произведение первых n чисел и предела.
Цитата(nosferatu @ 04 Apr 2013, 20:15)
Цитата(Terraniux @ 04 Apr 2013, 14:34)
Пока все думают, вот еще.
Сравните числа.
и
Вечером выложу решение, если ранее не решите.
Сравните числа.
и Вечером выложу решение, если ранее не решите.
Очевидно, что второе больше.
Корень из 1.5 примерно равен 1.225
Второе число будет стремиться к 1.17, можно примерно посчитать как произведение первых n чисел и предела.
Я вот извиняюсь, задача немного не та, что предполагалась. При записи допустил ошибку. Теперь верное условие.
Но можно подумать и о старом условии.
nosferatu, вот честно - неочевидно. Даже не понятно. Интуитивно кажется, что левое меньше, но все же надо построже.
Цитата(Terraniux @ 04 Apr 2013, 20:39)
Интуитивно кажется, что левое меньше, но все же надо построже.
Конечно надо. Эх, не ищи сложностей там, где их можно избежать, я поначалу пытался как-то через прогрессии и факториалы выразить.
Цитата(nosferatu @ 04 Apr 2013, 21:34)
Цитата(Terraniux @ 04 Apr 2013, 20:39)
Интуитивно кажется, что левое меньше, но все же надо построже.
Конечно надо. Эх, не ищи сложностей там, где их можно избежать, я поначалу пытался как-то через прогрессии и факториалы выразить.
Я тоже пока пробую через всякие сворачивания.
Посмотри измененную задачу. Она попроще должна быть.
Цитата(Terraniux @ 04 Apr 2013, 21:53)
Цитата(nosferatu @ 04 Apr 2013, 21:34)
Цитата(Terraniux @ 04 Apr 2013, 20:39)
Интуитивно кажется, что левое меньше, но все же надо построже.
Конечно надо. Эх, не ищи сложностей там, где их можно избежать, я поначалу пытался как-то через прогрессии и факториалы выразить.
Я тоже пока пробую через всякие сворачивания.
Посмотри измененную задачу. Она попроще должна быть.
Вот её через замену и сворачивания можно решить. Но меня больше интересует как исхитриться и формулу составить для нахождения произведения типа
(1^x+d)*(2^x+d)...((n-1)^x+d)*(n^x+d)
Цитата(Terraniux @ 04 Apr 2013, 14:34)
Сравните числа.
и
и А вот эта задача мне кажется одной из лучших моих.
Деревянный многогранник, вписанный в сферу, и описанный около сферы, распилил плоской пилой на 2 многогранника. Оказалось, что каждый из новых многогранников также является вписанным и описанным. Чему может равняться количество граней исходного многогранника?
Могу решение выложить, кому интересно.
Одним разрезом?
Цитата(nosferatu @ 05 Apr 2013, 22:52)
Одним разрезом?
Эм, каким макаром можно сделать более 1-го разреза и получить 2 новых многогранника?
Цитата(Terraniux @ 05 Apr 2013, 22:56)
Цитата(nosferatu @ 05 Apr 2013, 22:52)
Одним разрезом?
Эм, каким макаром можно сделать более 1-го разреза и получить 2 новых многогранника?
Если разрезать не до конца.
Цитата(nosferatu @ 05 Apr 2013, 22:58)
Цитата(Terraniux @ 05 Apr 2013, 22:56)
Цитата(nosferatu @ 05 Apr 2013, 22:52)
Одним разрезом?
Эм, каким макаром можно сделать более 1-го разреза и получить 2 новых многогранника?
Если разрезать не до конца.
Не, это за разрез не считается. Конкретнее - один разрез.
Ладно, пакеда. Завтра выложу под катом решение (или в личку заинтересовавшимся).
И каждый новый многоугольник "описанный" в геометрическом смысле?
Цитата(nosferatu @ 05 Apr 2013, 23:09)
И каждый новый многоугольник "описанный" в геометрическом смысле?
Многогранник - да.
Описался, да многогранник.
Теперь ты описан вокруг многогранника. 
Цитата(tolich @ 06 Apr 2013, 08:12)
Теперь ты описан вокруг многогранника.
Нет, это многогранник описан вокруг меня. Я же описался многогранником.
П.С.
А многогранник должен быть описан именно вокруг тех сфер и многогранников, которые уже есть/получены после разреза, или потенциально возможны быть описанными вокруг сфер, как написал Толич? Если второе, то задача элементарна, если первое, то у меня складывается впечатление, что её решить невозможно.
П.П.С. Ну, вы тоже подумайте над головоломкой:
У вас есть пять банок с пилюлями и электронные весы, которые показывают точный вес. Все настоящие пилюли весят по 1 грамму, все фальшивые весят по 2 грамма. В одной из банок только фальшивые пилюли, в четырёх других настоящие. Как определить, в какой из банок фальшивые пилюли за 1 (одно) взвешивание.
Количество пилюль в банках неизвестно, но их много и в разных банках может быть разное количество пилюль.
Цитата(tolich @ 06 Apr 2013, 07:50)
Есть подозрение, что это тетраэдр, разрезанной по одной из граней, так что обе части тоже тетраэдры.
Возьмём трёхграный угол, повернём вершиной вниз и кинем туда шар, он будет скатываться, пока не коснётся сразу всех граней. А теперь надуем или сдуем этот шар, пока он не коснётся противоположной углу грани. Готово, у нас вписанная сфера. Таким образом, в любой тетраэдр можно вписать сферу. (Ну на описать вокруг — само собой, через 4 точки не на одной плоскости всегда проведётся ровно одна сфера.)
Возможен ли такой фокус с другими многогранниками, не уверена. Предполага отрицательный ответ.
Возьмём трёхграный угол, повернём вершиной вниз и кинем туда шар, он будет скатываться, пока не коснётся сразу всех граней. А теперь надуем или сдуем этот шар, пока он не коснётся противоположной углу грани. Готово, у нас вписанная сфера. Таким образом, в любой тетраэдр можно вписать сферу. (Ну на описать вокруг — само собой, через 4 точки не на одной плоскости всегда проведётся ровно одна сфера.)
Возможен ли такой фокус с другими многогранниками, не уверена. Предполага отрицательный ответ.
Не, то что тетраэдр таким свойством обладает - это правда, спору нет. Но вопрос в том, сколько вообще может быть у этого многогранника граней. 4, как уже все поняли, может быть. А еще?
Кстати, в условии при переписывании опять немного пропущено: попробуйте порешать, если дополнительно известно, что у них разное число граней.
nosferatu, каждый из новых многогранников,
Каждый из новый многогранников является вписанно-описанным, в свою и около своей (никаких других требований насчет сфер не предъявляется).
Цитата(nosferatu @ 06 Apr 2013, 08:21)
П.П.С. Ну, вы тоже подумайте над головоломкой:
У вас есть пять банок с пилюлями и электронные весы, которые показывают точный вес. Все настоящие пилюли весят по 1 грамму, все фальшивые весят по 2 грамма. В одной из банок только фальшивые пилюли, в четырёх других настоящие. Как определить, в какой из банок фальшивые пилюли за 1 (одно) взвешивание.
Количество пилюль в банках неизвестно, но их много и в разных банках может быть разное количество пилюль.
У вас есть пять банок с пилюлями и электронные весы, которые показывают точный вес. Все настоящие пилюли весят по 1 грамму, все фальшивые весят по 2 грамма. В одной из банок только фальшивые пилюли, в четырёх других настоящие. Как определить, в какой из банок фальшивые пилюли за 1 (одно) взвешивание.
Количество пилюль в банках неизвестно, но их много и в разных банках может быть разное количество пилюль.
В каждой банке строго один вид пилюль? (или настоящий, или фальшивый)
Цитата(Terraniux @ 06 Apr 2013, 08:46)
Не, то что тетраэдр таким свойством обладает - это правда, спору нет. Но вопрос в том, сколько вообще может быть у этого многогранника граней. 4, как уже все поняли, может быть. А еще?
Пирамида с четырёхугольным основанием, делим на две треугольные пирамиды. 5
Пирамида с пятиугольным основанием, делим на треугольную пирамиду и пирамиду с основанием - равнобедренной трапецией. 6
Пирамида с шестиугольным основанием, делим на две пирамиды с основаниями - равнобедренными трапециями. 7
Disregard that.
Цитата(tolich @ 06 Apr 2013, 11:52)
Цитата(nosferatu @ 06 Apr 2013, 13:07)
Цитата(Terraniux @ 06 Apr 2013, 08:46)
Не, то что тетраэдр таким свойством обладает - это правда, спору нет. Но вопрос в том, сколько вообще может быть у этого многогранника граней. 4, как уже все поняли, может быть. А еще?
Пирамида с четырёхугольным основанием, делим на две треугольные пирамиды. 5
Пирамида с пятиугольным основанием, делим на треугольную пирамиду и пирамиду с основанием - равнобедренной трапецией. 6
Пирамида с шестиугольным основанием, делим на две пирамиды с основаниями - равнобедренными трапециями. 7
Так какой все-таки итоговый ответ?
Кстати, в оригинале было еще требование - чтобы количество граней у 2-х новых было разным. Порешайте ее с этим условием.
Для просмотра полной версии этой страницы, пожалуйста, пройдите по ссылке.